Falken Azenis tread life study

Introduction and motivation

The Falken Azenis Sport is a high-performance summer street tire which has enjoyed considerable success in SCCA Solo 2 (autocross) classes which require a street tire (defined as UTQG treadwear of at least 140). While my car competes in H Stock, where competition tires are permitted, my current circumstances do not permit me to store dedicated racing wheels and tires, and my local competitors do not run competition tires at this time. Given the success of the Azenis, their low cost, and their availability in my car's 14-inch size, they seemed a natural choice for combined street and autcross use; I live in the Los Angeles area where summer tires can be used year-round. My primary concern for the tires was their longevity. Like most high-performance tires, tread life is sacrificed to provide high levels of grip. This is a common concern for people considering the Azenis, so I decided to monitor the treadwear carefully. The results are presented here.

Methodology

The tires were P195/60R14, the only available 14-inch size. The stock tire size for my Civic del Sol Si is P185/60R14, but Honda shipped P195/60R14 tires on the same wheels for the Civic del Sol VTEC. The wheels are 5.5 inches wide, which is the narrowest width that Falken recommends for this tire. Tread depths were measured using a Snap-On tread depth gauge, using the 1/32" scale. Measurements were made when the tires were new, and at irregular intervals thereafter (typically between 500 and 1000 miles). Each measurement consisted of readings taken on all four tires, from the outside, middle, and inside tread blocks of each tire (12 readings in total). These readings were averaged, and an uncertainty in the mean was computed using the standard deviation of the readings and an assumed 0.5/32" uncertainty in reading the gauge. Thus, the uncertainty in the mean of an averaged set of measurements is given by sqrt(Σ(σ_i² + 0.5²))/12, where σ_i is the deviation of each reading from the mean.

The tires were used for 12,022 miles and 102 autocross runs. They were rotated once, 8,130 miles after installation. My car is front-wheel-drive, so the front tires wear considerably faster than the rears. The car weighs approximately 2,400 pounds. Of the autocrosses, 26 runs were at an Evolution Phase 1 school on a short (30-second) course. 16 were at the Lone Pine Time Trials, on a 160-second course which is very hard on tires. The remainder were at Los Angeles-area autocrosses which are typically 75-100 seconds long. The street miles include a considerable amount of hard driving on mountain roads (perhaps 15-20% of the total miles). Front and rear toe were set to the maximum toe-out permitted by the manufacturer. Camber is not adjustable but is within specs (near zero). Tire pressures for the street were typically 32F/30R, slightly higher than Honda's spec of 29F/29R. Various pressures were used for autocross, typically around 40 psi cold.

Measurements and results

We can begin our analysis by plotting the depth measurements as a function of actual miles on the tires, and performing a linear least-squares fit to the data. Such a plot is shown below. The red points are the measurements, the green line is the fit, and the black lines indicate the total range of tread depths at each measurement.

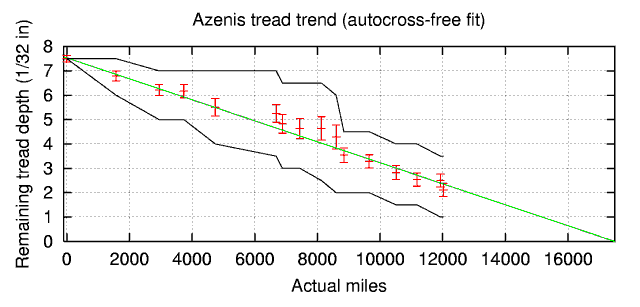
The wear rate for this fit is 2,321 miles per 1/32" of treadwear (±56 miles). Because the initial tread depth of 7.5/32" was a measured quantity, and hence subject to measurement error, the initial depth was also a free parameter in the fit, and the resulting value was 7.53/32" (±0.07/32"). The reduced chi-squared for this fit is χ²=0.63, indicating that our uncertainty estimates are too large. This is because the 12 contributing measurements are not normally distributed; they more closely follow a bimodal distribution, with distinct wear rates for the front and rear tires. Thus, the σ described above incorporates the difference in wear rates, which is a systematic rather than statistical effect.

You will note in the figure that there are several places where the depth decreases abruptly (e.g. 8,500 miles and 12,000 miles). This sudden tread wear is a result of concentrated autocross activity. We can attempt to model the accelerated wear by saying that one autocross run is worth C street miles, where C is a free parameter in the fit. We can measure tread depth against "effective miles," where an "effective mile" is either one street mile, or 1/C autocross runs. The results of such an attempt are shown below.

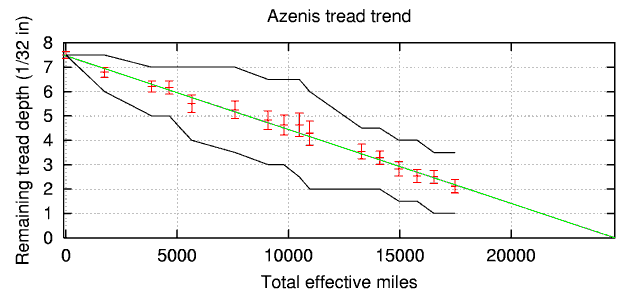
This approach has succeeded in linearizing the data. The results of this fit are that tread wear is 3,300 effective miles per 1/32" (±266 miles), and that an autocross run is worth 53 effective miles (±14 miles). The initial tread depth from the fit was 7.47/32" (±0.04/32"). This result may be useful to new autocrossers who wonder how hard autocrossing is on tires (although it is important to note that non-performance tires may fare worse, due to overheating and chunking). We can see from this plot that I retired the Azenis at about 17,500 effective miles. This suggests that if I did not use them for autocrossing, they would last about that many miles on the street.

It is possible to improve our measurement of C, the effective miles per autocross run. In fitting the plot above, C and the tread wear rate are degenerate, because the number of autocross runs on the tires generally increases in proportion to the total miles on the tires. We can instead measure the wear rate and C by plotting for each measurement interval the amount by which the tread depth decreased. This is a noisy data set, because the tread wear from one measurement to the next is similar to the uncertainty in that measurement, but it breaks the degeneracy: Some intervals consist only of street miles (no autocross runs), and others consist mostly of autocross runs. The plot is shown below.

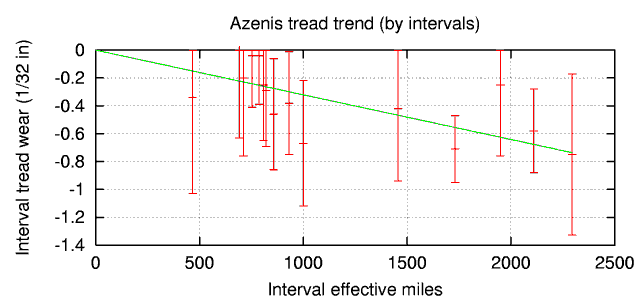
This fit gives C=52 miles per 1/32" (±19 miles), in good agreement with the previous result, but the correlation matrix for this fit indicates that C is much less degenerate with the wear rate (0.680 vs. 0.984).

Conclusions and future directions

We have found that the wear rate for the Azenis on the test vehicle was 3,300 effective miles (corresponding to street miles) per 1/32" of treadwear, and that an autocross run resulted in wear equivalent to 53 miles of street driving. The tires were removed from service at about 17,500 effective miles of service, when the minimum measured tread depth was 1/32". In dry conditions, or for competition use, they could be used longer, but in wet conditions an earlier replacement is recommended.

A second, identical set of tires has been installed on the test vehicle, and will contribute more measurements to the above data. Additional types of tires may be tested in the future.